
Have you ever wondered what would happen if all the people in the world were put into a really big blender and turned on? Since all the individuals on Earth would be blended together, what would be the size of the resulting mass?

With this question in mind, a Reddit user tries to do the math. However, the truth might not align with your imagination. The resulting human goo ball isn't as big as you might think. So, what would be the size of the resultant mass?
A Reddit user by the name of kiwi2703 undertook the task of performing the calculations. In the post, user wrote:
If you blended all 7.88 billion ppl on Earth into a fine goo (density of a human=985 kg/m3, average human body mass=62 kg), you would end up with a sphere of human goo just under 1 km wide. This is a visualization of how that would look like in Central Park.
As a result, this sphere of goo would have a diameter of slightly less than 1 kilometer (approximately three times the height of the Eiffel Tower), and it could easily fit into Central Park in New York City.

With all the people living in the world, this sphere is actually quite small, highlighting the astonishing extent to which Earth's resources have been altered to provide for this goo ball.

Although this issue might be a bit gross, it's not the first time that numerous people have expressed curiosity about the space humans occupy on Earth. Back in 2015, it was demonstrated that the world's population, which was 7.3 billion individuals at the time, could fit within the confines of New York City.
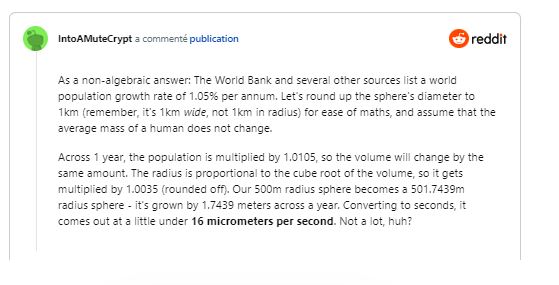
Considering this, if the human meatball continues to grow in the future, Redditor IntoAMuteCrypt has arrived at an answer using data sourced from The World Bank.
"As a non-algebraic answer: The World Bank and several other sources list a world population growth rate of 1.05% per annum. Let's round up the sphere's diameter to 1km (remember, it's 1km wide, not 1km in radius) for ease of maths, and assume that the average mass of a human does not change.
Across 1 year, the population is multiplied by 1.0105, so the volume will change by the same amount. The radius is proportional to the cube root of the volume, so it gets multiplied by 1.0035 (rounded off). Our 500m radius sphere becomes a 501.7439m radius sphere – it's grown by 1.7439 meters across a year. Converting to seconds, it comes out at a little under 16 micrometers per second. Not a lot, huh?"
What are your thoughts on this fascinating topic?




